Day: October 17, 2015

DATA:

Speed (RPM)	Battery Discharge (mV)	Mass (kg)	Power Level (%)	Time (s)	Acceleration (RPM/s^2)	height (m)	g	Potential Energy (J)	Power (W)
101.8302	69	0.25	75	4.28	23.792107	0.25	9.81	0.613125	0.143254
81.02994	41	0.25	75	2.026	39.995037	0.25	9.81	0.613125	0.302628
83.21144	69	0.25	75	2.051	40.571156	0.25	9.81	0.613125	0.29894
90.48324	41	0.19	75	2.028	44.61698	0.25	9.81	0.465975	0.229771
92.49195	27	0.13	75	1.656	55.852626	0.25	9.81	0.318825	0.192527
97.0276	27	0.07	75	1.57	61.80102	0.25	9.81	0.171675	0.109347
99.26762	27	0.07	75	1.684	58.947516	0.25	9.81	0.171675	0.101945
47.24775	41	0.25	50	3.591	13.157268	0.25	9.81	0.613125	0.170739
81.71883	55	0.25	75	2.013	40.595543	0.25	9.81	0.613125	0.304583
102.8455	83	0.25	90	1.64	62.710688	0.25	9.81	0.613125	0.373857
125.0974	55	0.25	100	1.283	97.503841	0.25	9.81	0.613125	0.373857

---

 

Explore Newton’s 2nd Law

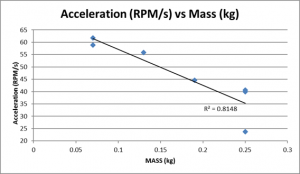
Keeping the power level fixed and changing the mass.  Does the acceleration vary with mass?

 

Increasing mass decreases acceleration. This agrees with Newton’s Law F = ma. If F is staying constant, as mass increases, acceleration must decrease to balance it out.

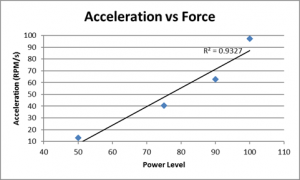
Keep the mass fixed and change the power level.  Does the acceleration vary with power level?

Increasing the power level does increase the acceleration. Again, looking at F = ma, if F is increasing, yet mass is staying the same, acceleration must also increase in order to keep both sides of the equation equal.

Explore the Law of Conservation of energy

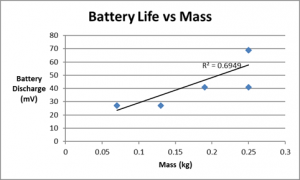
With the power level fixed, study how the battery energy drainage changes as a function of mass.  Since the energy of the battery is converted to the potential energy of the masses, you would expect that the greater the masses, the greater is the battery drainage.  However, the battery level reading is not that accurate, so you should repeat your measurements several times and look at the average battery drainage as a function of mass.

 

Our chart supports the theory that as mass increases the discharge of the battery also decreases. In other words, a heavier mass will cause the battery to drain more because of the increase of power required to raise it up a certain height. Work equals force multiplied by displacement. A larger mass means a larger force will be required meaning a larger amount of work. This work is what causes the battery to drain faster. Imagine it like this. Imagine trying to give a piggy-back ride to a child to the top of a hill versus trying to give a piggy-back ride to a full grown adult to the top of the same hill. The distance you have to travel is the same, but a lot more work is going to be needed to carry the adult all the way up, and as a result you will be a lot more tired by the time you get to the top. You’re lack of energy once reaching the top is the same as the battery being drained.

Calculate the average power used by the motor for each of your experiments.  For the same mass, plot power used as a function of the power level of the motor.  Add a linear trend line (with equation and R2 indicated).  Describe this curve.  Is it what you expected?

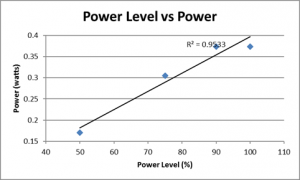
Yes this graph is what you would expect from this situation. Increasing the power level of the motor would also increase the power. We know that Power = Energy / time AND  Force = Mass * Acceleration AND Work = Force * Displacement. Knowing these three equations we can figure out that this is what is to be expected. Increasing the power level is the same thing as increasing the force. This increased force increases the work done by the pulley. With work and energy being basically the same thing for our purposes (technically they both have the same magnitude, just different signs – or +), increasing the energy means the overall power of the equation will also increase. To add on even more to this, increasing the power level also decreases the time. So in the power equation the numerator is increased while the denominator is decreased, making the power even larger.

Through this experiment and graphs we are supporting Newton’s theory of force and laws of conservation of energy.

The Mildred F Sawyer Library is one of two of Suffolk University’s amazing libraries.Too many students it’s almost like a second home because of the many hours spent there grinding out homework after homework after project after project. There are three floors to the Sawyer Library each with different uses and resources at the disposal of the student body.

The first floor is the main entrance and lobby area. The checkout desk is at the entrance where of course books can be checked out of the library. However, it is not limited to just that, other useful items such as laptops and even phone chargers can be checked out for use if you are ever in the need for them. The lobby area also contains many desktops also available for use for any students. At the back wall, there is the reference desk. The reference desk is where to go if you have any questions to anything related to the library or books. There are three printers on this floor for use as well. To the right of the reference desk are reference books which can help you find other potential books that may be useful for you in every field imaginable. Another feature that you will notice immediately that this is the lively and talkative floor of the library. If you want to chill, talk with friends, but perhaps still do a bit of work, this is a good floor to be on because no one will scold you for talking.

 

The second floor is for students who wish to get more work done and be more productive, yet still be able to collaborate with other students in a quiet manner. The second floor features several study rooms which can be reserved on the Suffolk Library page.Definitely a good room to have as a resource if you need to work on group projects, especially with the access to the whiteboards. Just remember that the rumors stating the those rooms are soundproof are false. But unless you are yelling, I don’t believe anyone will hear you talking (or watching youtube videos, your choice). There are also classrooms on the second floor with computers. Here we were taught about the many resources available to us online on the Suffolk Library website. There are tons of small details that can be very useful, but the list would go on and on if I tried telling you every single thing. You will discover them in your time at Suffolk. I will focus on two main things. The search engine which allows you to filter through many books and even ebooks on different subjects, and can direct you to other possible books of interest depending on your previous search. The ebooks are also available to read online free of charge, all you have to do is find it and click a link. The second important feature is the MASSIVE database. To anyone who has ever had to write a research paper, you should know what databases are. There are pools of different articles, literary criticisms, blogs etc, that can potentially be used in research papers and other types of papers as well. Or even, just to learn more about certain topics. The filters on these databases allow you to cut a search of, let’s say, “energy and sustainability” from 11,000 results to a mere hundred or less. Every student at Suffolk will become familiar with these databases.

 

Finally the third floor, not as much to say as the previous two floors, but still important nonetheless. Taking a journey to the third floor should only be undergone by the most serious of students. You procrastinated a paper for your class, and it’s due in a couple hours. Go to the third floor. Didn’t do the past five assignments for a class and you need to get it done before you fail? Go to the third floor. The third floor is the floor of pure silence. If you need to focus, go to this floor. Nothing will distract you. f you talk, you’re probably distracting someone else. I myself have never dared to take the trip to the third floor, for that is a trip for the extreme players of this game called college. I have only heard the tales of the third floor. One day I will be brave enough to attend it, one day….one day.

 

Alright, that’s my blog. Thanks for reading!